Overdispersed data
Last updated on 2026-02-24 | Edit this page
Estimated time: 20 minutes
Overview
Questions
- Which models account for biological variability?
Objectives
- Provide a workflow for modeling count additional variability
NOTE: This episode is work in progress.
For the theory in this section, see this study.
The data for this episode
I simulate data that has the same structure and covariates as in the last episode, but different counts:
- Again, we have
roundandstretchedas possible cell shapes. - We compare the fraction of round and stretched in a control and
treatment
condition. - There are three replicates of the resulting \(2\times 2\) table.
- I simulate negative binomial cell counts where
- the probability of a cell being round is constant \(p=1/3\) in all replicates and conditions.
- I.e.: Neither treatment nor replicate have an effect.
In biological terms, imagine we have new data of the same type, but unlike last time, replicates are now taken on different days by three different technicians.
data generation
R
set.seed(4)
mysize <- 2
ctrl_round <- rnbinom(3,size =mysize , mu = 10)
ctrl_stretched <- rnbinom(3, size = mysize, mu=20)
trt_round <- rnbinom(3, size = mysize, mu= 10)
trt_stretched <- rnbinom(3, size=mysize, mu=20)
cells2 <- data.frame(
condition = c(rep("ctrl",6), rep("trt",6)),
shape = rep(c(rep("round",3), rep("stretched",3)),2),
count = c(ctrl_round, ctrl_stretched, trt_round, trt_stretched),
replicate = rep(c("1","2","3"),4)
)
This is what the data looks like.
R
cells2
OUTPUT
condition shape count replicate
1 ctrl round 7 1
2 ctrl round 5 2
3 ctrl round 11 3
4 ctrl stretched 3 1
5 ctrl stretched 59 2
6 ctrl stretched 22 3
7 trt round 9 1
8 trt round 8 2
9 trt round 4 3
10 trt stretched 49 1
11 trt stretched 59 2
12 trt stretched 26 3We bring the data in a suitable format:
R
cells2F <- cells2 %>%
pivot_wider(
names_from = "shape",
values_from = "count"
) %>%
mutate(total = round + stretched) %>%
mutate(fraction = round/total)
cells2F$replicate <- factor(cells2F$replicate)
cells2F
OUTPUT
# A tibble: 6 × 6
condition replicate round stretched total fraction
<chr> <fct> <dbl> <dbl> <dbl> <dbl>
1 ctrl 1 7 3 10 0.7
2 ctrl 2 5 59 64 0.0781
3 ctrl 3 11 22 33 0.333
4 trt 1 9 49 58 0.155
5 trt 2 8 59 67 0.119
6 trt 3 4 26 30 0.133 We add a variable called obs for “observation”. Each
fraction of round cells is an observation in this experiment. We’ll need
this variable for modeling variability.
R
cells2F <- cells2F %>%
mutate(obs = factor(1:n()))
cells2F
OUTPUT
# A tibble: 6 × 7
condition replicate round stretched total fraction obs
<chr> <fct> <dbl> <dbl> <dbl> <dbl> <fct>
1 ctrl 1 7 3 10 0.7 1
2 ctrl 2 5 59 64 0.0781 2
3 ctrl 3 11 22 33 0.333 3
4 trt 1 9 49 58 0.155 4
5 trt 2 8 59 67 0.119 5
6 trt 3 4 26 30 0.133 6 Binomial model
Start by setting up a model as in last episode:
R
binomial.model <- glm( cbind(round,stretched) ~ condition + replicate ,
data= cells2F,
family= binomial("logit")
)
summary(binomial.model)
OUTPUT
Call:
glm(formula = cbind(round, stretched) ~ condition + replicate,
family = binomial("logit"), data = cells2F)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.4504 0.4182 -1.077 0.28151
conditiontrt -0.8821 0.3770 -2.340 0.01930 *
replicate2 -1.3813 0.4481 -3.083 0.00205 **
replicate3 -0.3438 0.4491 -0.765 0.44401
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 25.212 on 5 degrees of freedom
Residual deviance: 10.495 on 2 degrees of freedom
AIC: 39.205
Number of Fisher Scoring iterations: 4Model assumptions:
- This model allows the fraction to vary by replicate
- We assume the replicate doesn’t change how the condition impacts the
fractions (otherwise there would be an interaction between
replicateandcondition). - We don’t assume variability on the observation level that goes beyond binomial variability.
Model finding:
- According to
binomial.model, the fractions are significantly different for control and treatment (in each replicate). The Wald test forconditiontrtgives \(p = 0.019\).
We can now check for overdispersion, based on this model:
R
library(performance)
check_overdispersion(binomial.model)
ERROR
Error:
! Package `DHARMa` required for this function to work.
Please install it by running `install.packages("DHARMa")`.This test doesn’t find sufficient evidence for overdispersion – which
doesn’t mean it’s not present. Overdispersion in this case means that on
top of the between-replicate variability, the fractions vary on the
observation level. It is hard to detect, because a lot of the
variability will be attributed to the replicate variable in
the model.
We can check visually:
R
cells2F %>%
ggplot(aes(x=condition, y=fraction))+
geom_point()
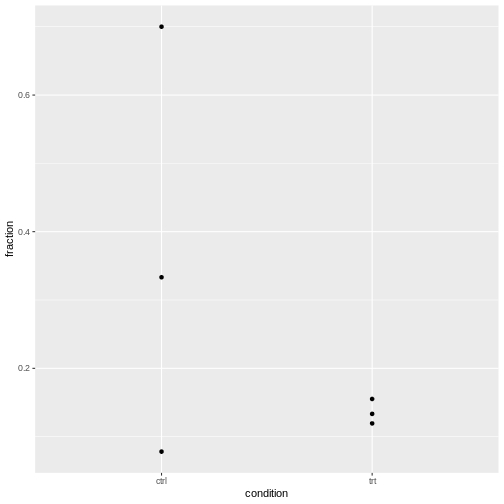
We should account for the overdispersion, to ensure the differences between control and treatment were not due to overdispersion.
Including overdispersion in models
We try two ways:
- observation-level random effects
- Beta-binomial model
OLRE
Fit linear model with random effect replicate observation level (OLRE). This is accounting for unmodeled, random variability at the observation level (replicate).
R
library(lme4)
glmer.olre <- glmer(cbind(round,stretched) ~ condition + (1|replicate) + (1|obs),
data= cells2F,
family= binomial("logit"))
This model has two random effects:
-
(1|replicate)for the effect of the replicate on fractions. -
(1|replicate:condition): observation-level random effect (fractions are allowed additional variability within the replicates)
R
summary(glmer.olre)
OUTPUT
Generalized linear mixed model fit by maximum likelihood (Laplace
Approximation) [glmerMod]
Family: binomial ( logit )
Formula: cbind(round, stretched) ~ condition + (1 | replicate) + (1 | obs)
Data: cells2F
AIC BIC logLik -2*log(L) df.resid
43.4 42.5 -17.7 35.4 2
Scaled residuals:
Min 1Q Median 3Q Max
-0.83577 -0.02100 0.04574 0.12325 1.14415
Random effects:
Groups Name Variance Std.Dev.
obs (Intercept) 0.4256 0.6523
replicate (Intercept) 0.1388 0.3725
Number of obs: 6, groups: obs, 6; replicate, 3
Fixed effects:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.9341 0.5184 -1.802 0.0715 .
conditiontrt -0.9657 0.6547 -1.475 0.1402
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
conditintrt -0.660The OLRE model estimates a variance for both random effects. Note that it attributes the majority of the variance to the observations, not the replicate. This implies that obser
Betabinomial model
The betabinomial mode below - models the replicate as a random effect (drawn from a normal distribution), - and on top of that, it assumes that individual probabilities (on the observation level) are drawn from a betabinomial distribution.
Citing from Harrison, 2015:
“[…] instead of drawing observed counts directly from a Binomial distribution with mean \(p_i\), we draw the Binomial probabilities from a beta distribution with parameters \(a\) and \(b\):
\(\text{beta}.p_i ~ \text{Beta}(a_i, b_i)\)
\(a_i = \frac{p_i}{\phi}\)
\(h_i ~ \text{Binomial}(c_i, \text{beta}.p_i)\)”
Load required library:
R
library(glmmTMB)
Set up the model and look at the summary:
R
model.glmmTMB <- glmmTMB(cbind(round,stretched) ~ condition + (1|replicate),
family=betabinomial(link = "logit"),
data=cells2F)
R
summary(model.glmmTMB)
OUTPUT
Family: betabinomial ( logit )
Formula: cbind(round, stretched) ~ condition + (1 | replicate)
Data: cells2F
AIC BIC logLik -2*log(L) df.resid
44.2 43.4 -18.1 36.2 2
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
replicate (Intercept) 0.217 0.4659
Number of obs: 6, groups: replicate, 3
Dispersion parameter for betabinomial family (): 22.1
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.8986 0.4747 -1.893 0.0584 .
conditiontrt -0.9135 0.6060 -1.508 0.1317
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Finding Both models conclude that there is no difference in the fraction of round cells between control and treatment. Accordingly, in the data generation process, I used equal fractions. None of the model is perfect in telling where the variability is coming from. They both attribute some of the variability to the replicate, which was not how the data was generated.
