Pairwise comparisons
Last updated on 2024-07-16 | Edit this page
Estimated time: 12 minutes
Overview
Questions
- What are pairwise comparisons, and how do they relate to the broader concept of multiple testing in statistical analysis?
- How can we effectively conduct and interpret pairwise comparisons to make valid statistical inferences while controlling for the family-wise error rate?
Objectives
- Understand the Concept of Pairwise Comparisons
- Learn how to conduct and interpret Pairwise Comparisons
Pairwise comparisons
Pairwise comparisons are a fundamental concept in statistical analysis, allowing us to compare the means or proportions of multiple groups or conditions. In this episode, we will explore the concept of pairwise comparisons, their importance in statistical testing, and how they relate to the broader context of multiple testing.
Understanding Pairwise Comparisons
In our example of air pollution, fine particulate matter and other pollutants can induce systemic inflammation in the body, leading to an increase in circulating inflammatory markers like C-reactive protein (CRP). Suppose we decide to divide the population into four groups based on different levels of exposure to air pollution. Lets assume these groups are as follow:
- Low exposure: Individuals living in rural areas with minimal industrial activity and low traffic density.
- Moderate exposure: Individuals living in suburban areas with some industrial activity and moderate traffic density.
- High exposure: Individuals living in urban areas with significant industrial activity and high traffic density.
- Very high exposure: Individuals living near industrial zones, major highways, or heavily polluted urban areas.
Table 2 shows the first six rows of CRP values of individuals in the four exposure groups.
| CRP | Exposure |
|---|---|
| 1.379049 | Low_exposure |
| 2.039645 | Low_exposure |
| 5.617417 | Low_exposure |
| 2.641017 | Low_exposure |
| 2.758576 | Low_exposure |
| 5.930130 | Low_exposure |
In this case the “Exposure” column is a categorical variable with four groups of exposure levels (Low_exposure, Moderate_exposure, High_exposure, and Very_high_exposure).
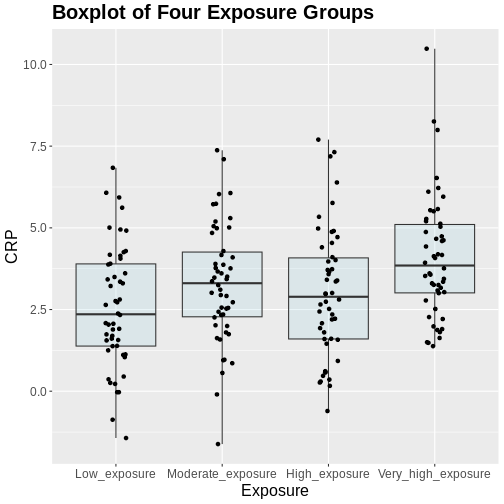
Generally, from the above plot, as exposure level increases from low to very high, we might expect to see a corresponding increase in the median exposure level and higher median C-reactive protein (CRP) values.
Our null hypothesis is that there is no difference in CRP amounts in the different groups. Our significance levels is 0.05.
First we would do ANOVA, which would tell us whether there are any differences between the groups.
OUTPUT
Df Sum Sq Mean Sq F value Pr(>F)
Exposure 3 60.8 20.268 5.754 0.00086 ***
Residuals 196 690.4 3.523
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The ANOVA output above, shows statistically significant differences among the means of the four exposure groups. It does this by comparing the variability within each group to the variability between the groups. We therefore reject the null hypothesis of equal means.
Why do we need multiple comparisons?
ANOVA alone does not tell us which specific groups differ significantly from each other. To determine this, we need to conduct further analysis. Multiple comparison procedures (also known as post-hoc tests) are used to compare pairs of groups in order to identify where the differences lie. These tests provide more detailed information about which specific group means are different from each other.
Methods for Performing Pairwise Comparisons
Parametric methods, such as ANOVA post-hoc tests (e.g., Tukey’s HSD) are used when assumptions of normality and homogeneity of variance are met. Non-parametric methods, such as pairwise Wilcoxon tests, are suitable when data do not meet the assumptions of parametric tests. In R, performing pairwise comparisons is straightforward using built-in functions and packages.
OUTPUT
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = CRP ~ Exposure, data = data)
$Exposure
diff lwr upr p adj
Moderate_exposure-Low_exposure 0.7240094 -0.2486521 1.6966710 0.2193881
High_exposure-Low_exposure 0.4233920 -0.5492695 1.3960536 0.6727404
Very_high_exposure-Low_exposure 1.5088066 0.5361450 2.4814681 0.0004795
High_exposure-Moderate_exposure -0.3006174 -1.2732790 0.6720442 0.8539510
Very_high_exposure-Moderate_exposure 0.7847971 -0.1878644 1.7574587 0.1597266
Very_high_exposure-High_exposure 1.0854145 0.1127530 2.0580761 0.0219956We perform a Tukey post-hoc test using TukeyHSD() to determine which specific exposure group means differ significantly from each other. The results provide pairwise comparisons of group means along with adjusted p-values to account for multiple comparisons.
Interpreting Pairwise Comparison Results
Understanding significance levels and p-values obtained from pairwise comparisons is essential for interpreting results accurately. The p-values obtained from pairwise comparisons using the Tukey test are adjusted to control the familywise error rate (FWER). Adjusted p-values reflect the probability of observing a given result (or more extreme) under the assumption that all null hypotheses are true, while accounting for the number of comparisons made. Here, we interpret pairwise comparison results with adjusted p-values from the Tukey test by assessing whether the adjusted p-value is less than the chosen significance level (α) (0.05). If the adjusted p-value is below the significance level, we conclude that the observed difference is statistically significant after correcting for multiple comparisons.
In some research scenarios, the comparisons between groups are designed to answer specific, pre-defined research questions that are not directly addressed by traditional ANOVA and subsequent p-value adjustments. In this case, ANOVA and p-value adjustment don’t make any sense.
For example, imagine we are conducting a study to investigate the effect of different types of exercise (A, B, C, D) on three different health outcomes (X, Y, Z). Our primary interest here is to compare each type of exercise directly with respect to each health outcome, rather than comparing all exercises together using ANOVA.
Probable research questions would be:
- Does exercise type A have a different effect than exercise type B on health outcome X?
- Is there a difference in the effect of exercise type A compared to exercise type C on health outcome Y?
- How does exercise type D compare to exercise type B in terms of health outcome Z?
In this case, instead of conducting a single ANOVA followed by post-hoc tests to compare all exercises simultaneously, each comparison is treated as a separate research question. The focus is on comparing specific pairs of exercise types for each health outcome.
This means that we would analyze each comparison (e.g., A vs B for X, A vs C for Y, D vs B for Z) independently using appropriate statistical tests suited for comparing two groups (e.g., t-tests, Wilcoxon rank-sum tests, etc.). Since these comparisons are independent and are addressing distinct research questions, there is no need for ANOVA or adjustment of p-values across comparisons.
We would then interpret the results of each pairwise comparison based on their individual statistical significance and effect sizes relevant to the specific research question posed. This approach allows for a focused investigation into the differences between specific pairs of exercise types and their effects on different health outcomes. This tailored approach ensures that the statistical analysis aligns closely with the specific objectives of the study, providing meaningful insights into the relationships between variables of interest.
What we learn
Pairwise comparisons involve comparing the means or proportions of every possible pair of groups or conditions in a dataset. These comparisons are used to identify specific differences between groups or conditions that may not be apparent from overall statistical tests (like the above case ANOVA). These comparisons play a crucial role in statistical testing, particularly in the context of multiple comparisons. They allow us to examine specific comparisons of interest while controlling for the overall familywise error rate. The comparisons are commonly used in various fields, including medicine, biology, social sciences, and economics, to compare treatment groups, experimental conditions, or categorical variables.
Data snooping 
In the context of the above analysis, data snooping refers to the practice of exploring the data extensively, testing multiple hypotheses, and making comparisons until finding a statistically significant result or an interesting pattern. This can lead to overfitting the data or finding false positives due to chance alone.
In our example, data snooping could involve testing multiple comparisons between exposure groups until finding one that appears to be statistically significant or interesting. For example, one might compare only the “Very_high_exposure” group with the other groups, ignoring other potential comparisons. This selective comparison increases the likelihood of finding a significant result by chance alone.
Additionally, in some cases, we might decide not to perform all tests. We could just visually inspect our plot, and only perform the test that seems most promising when comparing the bars by eye. For example, after observing the initial boxplot, we might want to conduct numerous additional analyses or subgroup comparisons based on observed patterns, without pre-specifying these comparisons. This approach can lead to inflated Type I error rates (false positives) if corrections for multiple testing are not applied.
Data snooping can influence decision-making by focusing only on results that appear favorable or intriguing in the data. For instance, if a particular exposure group shows a larger mean than others, a decision might be made to focus solely on interventions or policies targeting that group without considering the broader context or potential confounding factors.
Additional resources
For further reading and hands-on practice with pairwise comparisons in R, refer to R documentation on pairwise comparisons, Applied Statistics with R and book by Oehlert 2010 resources.
Inline instructor notes can help inform instructors of timing challenges associated with the lessons. They appear in the “Instructor View”
