The QQ-plot

Overview

Questions

• What is the QQ-plot?
• How can I create a QQ-plot of my data?
• Why is it useful?

Objectives

• Demonstrate the calculation of quantiles in R.
• Explain the QQ-plot.
• Introduce functions to make a qq-plot in R.

The QQ-plot

---

The qq-plot compares the quantiles of two distributions.

Quantiles are the inverse of the cumulative distribution, i.e., the qnorm function is the inverse of pnorm:

You can use pnorm to ask for the probability of seeing a value of \(-2\) or smaller:

R

pnorm(q = -2,mean=0, sd=2) 

OUTPUT

[1] 0.1586553

Then you can use qnorm to ask that is the value for which 15% of the other values are smaller. Here, I demonstrate this by plugging the result into the pnorm function into the qnorm function:

R

qnorm(p= pnorm(q = -2,mean=0, sd=2), mean=0, sd=2) 

OUTPUT

[1] -2

Let’s compare the quantiles of the simulated frog sizes to the theoretical quantiles of a normal distribution. There are specialized functions for qq-plots, so we don’t have to calculate the theoretical values by hand:

R

data.frame(frog_sizes) %>% 
  ggplot(aes(sample=frog_sizes))+
  geom_qq()+
  geom_qq_line()

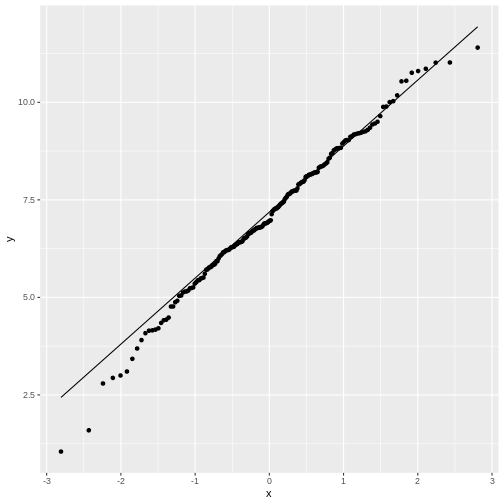
By default, the geom_qq function assumes that we compare to a standard normal distribution.
This fit doesn’t look too bad, although for low values the points stray away from the line. This shouldn’t surprise you, because remember: The normal distribution approximates the Poisson distribution (with which the simulation was generated) well for large values, but has limitations for low-valued counts.

Let’s set up a qq-plot where we compare to a Poisson distribution:

R

data.frame(frog_counts) %>% 
  ggplot(aes(sample=frog_counts))+
  geom_qq(distribution=qpois, dparams=list(lambda=mean(frog_counts)))+
  geom_abline()

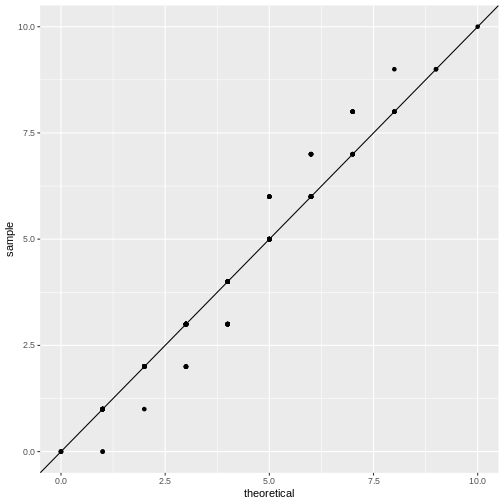
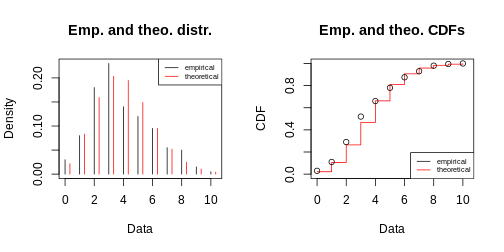
This fit looks better. We can still argue whether a qq-plot is the best representation for a Poisson fit, because due to the distribution’s discreteness, many data points end up on the exact same spot in the plot (overplotting). Thus, we loose information in this visualization.

One fits all - fitdistrplus package

---

If you want a quick overview, you can use the fitdistrplus package, which produces a series of plots.

Suppose you fit the frog counts to a normal distribution:

R

library(fitdistrplus)
my_fit <- fitdist(frog_counts, dist = "norm")
my_fit # gives you the parameter estimates

OUTPUT

Fitting of the distribution ' norm ' by maximum likelihood 
Parameters:
     estimate Std. Error
mean 3.830000  0.1495176
sd   2.114498  0.1057248

R

plot(my_fit)

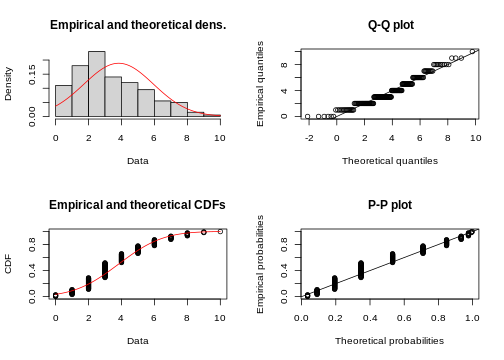
With some practice, this plot quickly allows you to see that you are comparing discrete data to a continuous distribution. Also, the QQ-plot doesn’t really give a straight line and the histogram seems to be skewed to the left, compared to theory.

Challenge

What does it look like if you fit the frog_counts to a Poisson instead?

Start from this set-up:

R

set.seed(51) # set a seed for reproducibility
frog_counts <-rpois(n = 200, lambda = 4)
library(fitdistrplus)

Show me the solution

R

my_fit <- fitdist(frog_counts, dist = "pois")
plot(my_fit)